题目
import libnum
import gmpy2
#生成素数
p=libnum.generate_prime(1024)
q=libnum.generate_prime(1024)
e1 = 2333
e2 = 23333
m = "flag{welc0me_t0_crypt0}"
m = libnum.s2n(m)
n= p * q
c1 = pow(m,e1,n)
c2 = pow(m,e2,n)
print("n1=",n)
print("e1=",e1)
print("c1=",c1)
print("n2=",n)
print("e2=",e2)
print("c2=",c2)
n1= 232386709436368212294181983036964840335465487253207895119051841544642165747413364204 621134762327433176742228667510937265639270464797770043359166623856543636719811459708 384817804673141226893181977655413390809439644017122880192619972788805693056098670729 951563699705413269178069248282662526715939950484425322050001738083273246890046229101 389729730208438997996300651271287958375819406567610589424021292872374186021462595358 497730335478976449715709075441544929289943903261810405141143808402498800962662132479 689095824813325194886611549303879663878262693954307608251386268674849319955795771388 60619071549478038088017447009
e1= 2333
c1= 182499511238279361651105801086265804955699834728862526475489209548137438888528301510 461700177812310917000331843742327357676592671529937806554190317880645730744328527374 211700186950915083126137917129685694260444460038935244999939424699240559176105814379 340183952059233657223080580607017535500026875597537417228974392611120146466402652598 516879384158293989418917112879153229506315159697692974885533880511950494988883557884 497669546643093284591585230262842223871386847773170173595063356178168248812155159258 340009300197191015275403255460513415452480048385279489924461992458151166774607778637 56165903160043717884206023382 n2= 232386709436368212294181983036964840335465487253207895119051841544642165747413364204 621134762327433176742228667510937265639270464797770043359166623856543636719811459708 384817804673141226893181977655413390809439644017122880192619972788805693056098670729 951563699705413269178069248282662526715939950484425322050001738083273246890046229101 389729730208438997996300651271287958375819406567610589424021292872374186021462595358 497730335478976449715709075441544929289943903261810405141143808402498800962662132479 689095824813325194886611549303879663878262693954307608251386268674849319955795771388 60619071549478038088017447009
e2= 23333
c2= 795513931626540345441086932455908667979245229108247829493862669645544050151877072089 061892471060061872889280500282629155430952824271855677879922093499795725259815652265 131607156857771710348436576167599464458168687444731880205259716735521027185069483393 008772069360109389029136711134295174857478278337997240012299161227378092927415332835 624925375559924862436222180469822907722270427843762050910840536640713984606042887446 449271344845880841096695340933959839938215727699780460128368760911636658156001224232 858920136464429117896528104264149851439835204097847326440194543577606575224052227385 7215764354822976705881386403
RSA共模攻击
在传统的 RSA 加密中,每个公钥由「模数」和「公钥指数」构成。假设我们有两个公钥,它们的模数N一模一样,但指数分别是e1和e2,如果这两个公钥用来加密同一个明文 M,会产生两份密文:
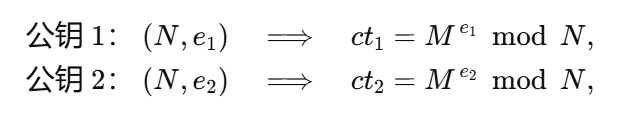
此时,如果e1和e2之间最大公约数是1,那么就能利用贝祖等式来直接求出明文M,不用分解N。贝祖等式:https://oi-wiki.org/math/number-theory/bezouts/


只要你有同一个模数、不同的指数,对同一个明文进行加密就能用数学方法把那两份密文合并回原文。
适用条件:
- 模数相同,两把公钥都使用了同一个N
- 指数不同,公钥指数e1e2不同,但必须同时满足下面第三条。
- 指数互素,e1e2的最大公约数为 1。如果它们不互素,则没法直接用贝祖等式解出明文。
- 同一明文重复加密,只有在加密对象相同的前提下,这两份密文才能对应到同一个明文M
- 密文可求逆,通常要求密文和N 也是互素关系,这保证了当需要用负幂时,可以找到乘法逆元。
题目随机生成了两个大素数 p 和 q(每个 1024 位),并令 n = p * q。
e1=2333 和 e2=23333 这两个不同的公钥指数,但都使用同一模数 n。 明文 m = flag{welc0me_t0_crypt0},通过 libnum.s2n(m) 转成数字(将字符串按照其字节序列视为一个大整数)。
使用不同的指数来加密同一个明文:
c1 = m^e1 mod n c2 = m^e2 mod n
把 n, e1, c1 和 n, e2, c2 打印出来。
从公开的 n, e1, c1 和 n, e2, c2 中解出原本的明文* m=flag{welc0me_t0_crypt0}*。
我们需要确认 e1=2333 与 e2=23333 互素(即 gcd(e1, e2) = 1)确保是不是可以使用共模攻击。再使用扩展欧几里得算法找出整数对 (x, y),满足 e1x + e2y = 1。
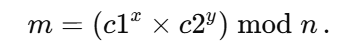
如果 x 或 y 为负数,需要先求相应密文的模逆,得到的 m 会是一个大整数,再把它转换成字节串,再解码成字符串;解码后就会看到flag{welc0me_t0_crypt0}。
扩展欧几里得算法的代码实现
from typing import Tuple
# 递归实现扩展欧几里得算法
def exEuclid(a, b) -> Tuple:
'''
return (x0,y0,gcd) contain a solution of ax + by == gcd(a,b) and gcd(a,b)
Notice:a should greater than b,otherwise will return a solution of bx + ay == gcd(a,b)
'''
(a, b) = (a, b) if a >= b else (b, a)
if b == 0 or a % b == 0:
return (0, 1, b)
(x1, y1, gcd) = exEuclid(b, a % b)
x0, y0 = y1, x1-(a//b)*y1
return (x0, y0, gcd)
代码
import math
n = 23238670943636821229418198303696484033546548725320789511905184154464216574741336420462113476232743317674222866751093726563927046479777004335916662385654363671981145970838481780467314122689318197765541339080943964401712288019261997278880569305609867072995156369970541326917806924828266252671593995048442532205000173808327324689004622910138972973020843899799630065127128795837581940656761058942402129287237418602146259535849773033547897644971570907544154492928994390326181040514114380840249880096266213247968909582481332519488661154930387966387826269395430760825138626867484931995579577138860619071549478038088017447009
e1 = 2333
c1 = 18249951123827936165110580108626580495569983472886252647548920954813743888852830151046170017781231091700033184374232735767659267152993780655419031788064573074432852737421170018695091508312613791712968569426044446003893524499993942469924055917610581437934018395205923365722308058060701753550002687559753741722897439261112014646640265259851687938415829398941891711287915322950631515969769297488553388051195049498888355788449766954664309328459158523026284222387138684777317017359506335617816824881215515925834000930019719101527540325546051341545248004838527948992446199245815116677460777863756165903160043717884206023382
e2 = 23333
c2 = 7955139316265403454410869324559086679792452291082478294938626696455440501518770720890618924710600618728892805002826291554309528242718556778799220934997957252598156522651316071568577717103484365761675994644581686874447318802052597167355210271850694833930087720693601093890291367111342951748574782783379972400122991612273780929274153328356249253755599248624362221804698229077222704278437620509108405366407139846060428874464492713448458808410966953409339598399382157276997804601283687609116366581560012242328589201364644291178965281042641498514398352040978473264401945435776065752240522273857215764354822976705881386403
g_e = math.gcd(e1, e2)
g_c1 = math.gcd(c1, n)
g_c2 = math.gcd(c2, n)
print("[verify] gcd(e1, e2) =", g_e)
print("[verify] gcd(c1, n) =", g_c1)
print("[verify] gcd(c2, n) =", g_c2)
def extended_gcd(a, b):
if b == 0:
return a, 1, 0
g, x0, y0 = extended_gcd(b, a % b)
x1 = y0
y1 = x0 - (a // b) * y0
return g, x1, y1
g, x, y = extended_gcd(e1, e2)
print("[verify] gcd(e1, e2) (again) =", g)
print("[verify] x =", x, ", y =", y)
print("[verify] e1*x + e2*y =", e1*x + e2*y)
m1 = pow(c1, x, n)
m2 = pow(c2, y, n)
M = (m1 * m2) % n
print("[verify] M =", M)
bit_len = M.bit_length()
byte_len = (bit_len + 7) // 8
plaintext_bytes = M.to_bytes(byte_len, 'big')
plaintext = plaintext_bytes.decode('utf-8')
print("[results]", plaintext)

[validate] M = 9810209026727229302391342816995339299030974665762025597
↑最终解密后得到的明文数值
接下来把这个大整数转换成字节,用 UTF-8 解码。
[results] flag{welc0me_t0_crypt0}