几乎是在过去十年里面NLP和序列建模的发展轨迹都是由《Attention Is All You Need》这篇提出的架构,确立了Self-Attention作为捕捉数据依赖关系的标准。
Attention Is All You Need将整个领域的研究重心从Recurrent和Convolutional归纳偏置,转移到了基于全局成对交互的模型上来作为现在大模型技术基石。但是现在模型规模的扩大和上下文窗口的无限延伸,《Attention Is Not What You Need》对显式自注意力机制的必要性提出了质疑,作者认为标准的多头注意力机制最好被理解为一种张量提升形式,这是一个数学上不透明的过程,它是将隐藏向量映射到一个高维的成对交互空间中。
虽然这个机制具有很高的表达能力,但是它受制于随序列长度平方增长的计算复杂度,且缺乏基于显式几何不变量的可解释性。作为替代方案这篇提出了因果格拉斯曼Transformer,这是一种用因果格拉斯曼混合层取代密集注意力矩阵的架构。
⬆️机制利用代数几何中的概念格拉斯曼流形和普吕克坐标,将信息流建模为低秩子空间的受控变形。由此产生的架构在固定秩的情况下实现了随序列长度线性扩展(O(L))的复杂度,并为神经推理提供了一条更严谨的几何路径 。
虽然现在格拉斯曼方法由于实现成熟度的问题,在Perplexity和实际运行时间上目前落后于Transformer,但是能给出新方向,序列建模的未来可能不在于暴力计算全局相关性,而是在有限维流形上学习结构化的、保持不变量的Flows。
序列建模史
在理解这篇提出的批评的量级之前,先回顾一下深度学习在序列建模领域的演进历史。
在2017年之前,序列建模的主导逻辑是Time Step,RNN 变体LSTM和GRU,通过维护一个隐藏状态ht,将历史信息压缩并传递到下一步,这种方法的归纳偏置是距离越近,关系越紧密,意味着顺序很重要。但是这种串行计算不仅阻碍了GPU并行计算能力的发挥,还有长程遗忘的问题,随着序列变长,早期的信息在反复的矩阵乘法和非线性激活中消散。
最经典的Transformer提出了一种激进的假设:放弃循环 拥抱并行。通过自注意力机制,序列中的每一个Token都可以直接与所有其他Token进行交互,无论它们在序列中的距离有多远。这种全局感受野让模型可以捕捉极其复杂依赖关系。
但是自注意力的核心计算涉及生成一个L X L的注意力矩阵,这意味着计算量和内存消耗都随着L的平方增长。
例如早期的机器翻译是L=512,计算量微不足道,当L=100000时计算量变得非常庞大。为了解决这个,有了很多的无数线性Attention变体,像是最近很火的Linformer和BigBird,他们都试图通过近似方法降低复杂度,但是大多数方法都在性能和精度上有所妥协。
在上述背景下的Attention Is Not What You Need提出了一种新的解决思路,它不再试图修补注意力矩阵,而是开始质疑是否根本不需要构建这个矩阵,论文引入了代数几何的工具,试图证明序列建模的本质可能不是点与点之间的加权求和,而是子空间在流形上的演化。
Attention Is All You Need
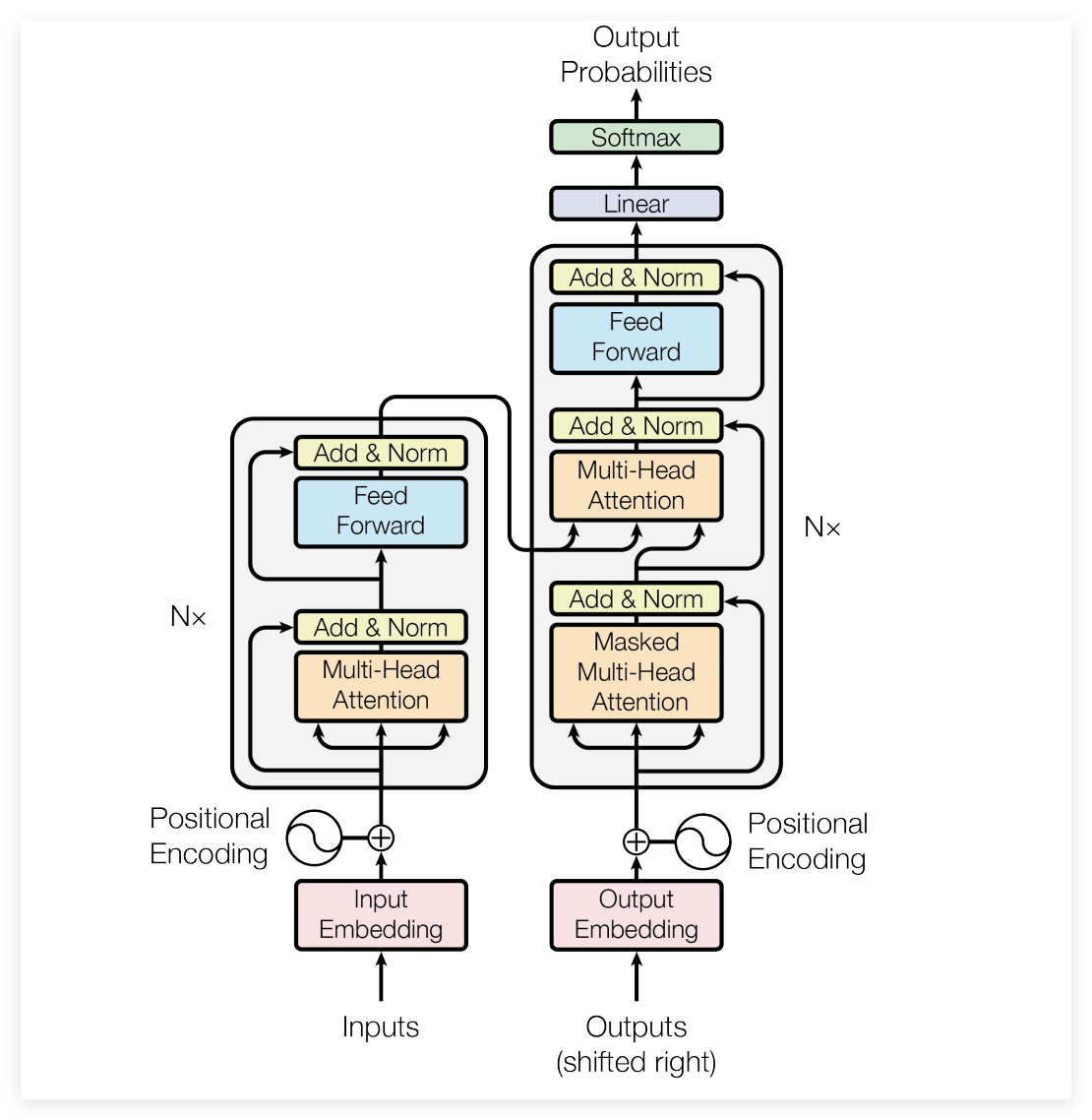
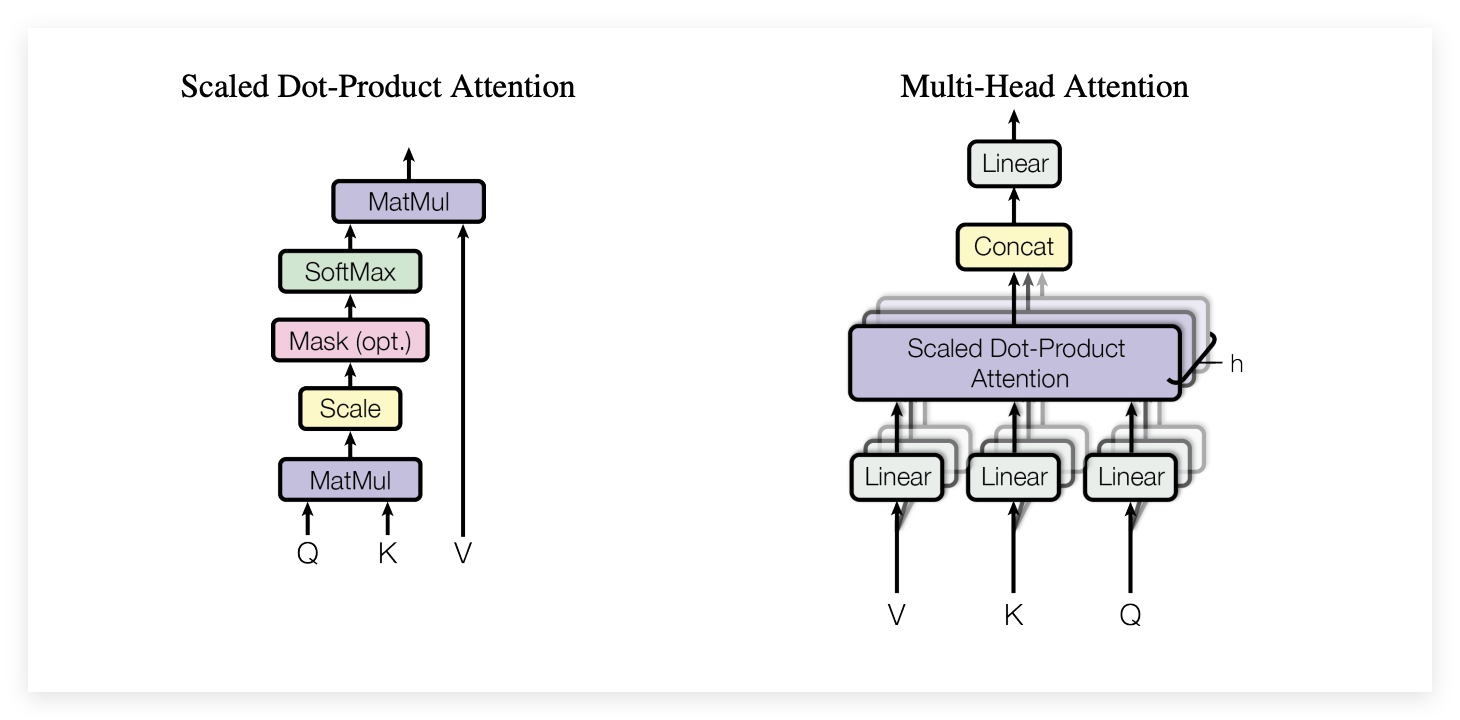
Transformer就是最小化归纳偏置转化为最大化的并行计算能力。
一是传统的RNN是串行的,必须等前一个词处理完才能处理下一个,Transformer移除了这种时间依赖,使整个序列的Token可以同时进入GPU进行矩阵运算,可以让在模型在大规模互联网语料上进行训练成为了可能。
第二个是位置编码,由于注意力机制是置换不变的,模型必须通过额外的方式告知每个词的位置,Transformer将语言视为一种带有位置标签的信息集合,而不是之前大多数的非严格的时间流。
Self Attention就是它的核心,它通过查询 键 指的隐喻,将语言处理演变为一种动态的信息检索过程,每个Token都在序列中寻找相关的线索,通过衡量语义特征的相似度来精准分配注意力。
这样让模型具备了内容寻址的能力,但是注意力成了一种竞争性资源,由于总量的归一化约束,模型对某一关联的深度聚焦必然伴随着对其他信息的淡化,为了确保在万亿级参数下的训练稳定性,缩放因子引入来化解了高维空间带来的计算饱和。
但是这种全连接的建模方式也埋下二次方复杂度的隐患,每个词都必须与序列中其他所有词进行两两比对,计算量和内存占用会随文本长度的增加是巨大的,像物理定律一样的限制让Transformer在处理长文档时还有有效率上的问题。
Transformer坚信只要数据与算力规模足够庞大,全连接的加权平均便能拟合万物,虽然在工程上取得了空前的成功,但是在效率的空白是巨大的,我们能不能找到一种数学结构,能承袭这种强大的全局建模能力,也能彻底摆脱二次方增长的计算原罪?
Attention Is Not What You Need
新的这篇引入了一个新的视角来审视注意力机制:张量提升。
作者认为自注意力的本质是将输入向量ht映射到一个高维的成对交互空间。提升是从d维向量空间到L^2维交互空间,在这个巨大的张量空间中模型通过梯度下降来约束张量的值,由于自由度极高,在这个空间中很难找到简单的数学不变量,所以我们很难用简洁的公式描述模型到底学到了什么 。
真正的智能推理应该具有结构化的几何特征,而不是在一个无约束的高维张量空间中漫游。
为了替代张量提升这里提出使用格拉斯曼流形作为计算的基础。

格拉斯曼流形
格拉斯曼流形Gr(k, n)意味着模型从点到结构变化,在传统的机器学习中将一个词看作向量空间中的一个孤立点,但在格拉斯曼流形研究的对象变成了子空间,即所有通过原点的k维平面。
如果说单个向量是描述某个概念的孤立坐标,那么格拉斯曼流形就是这些坐标所能编织出的所有关系网,模型处理的一等公民不再是碎片化的词汇,而是词与词之间通过交互形成的几何结构。
普吕克坐标
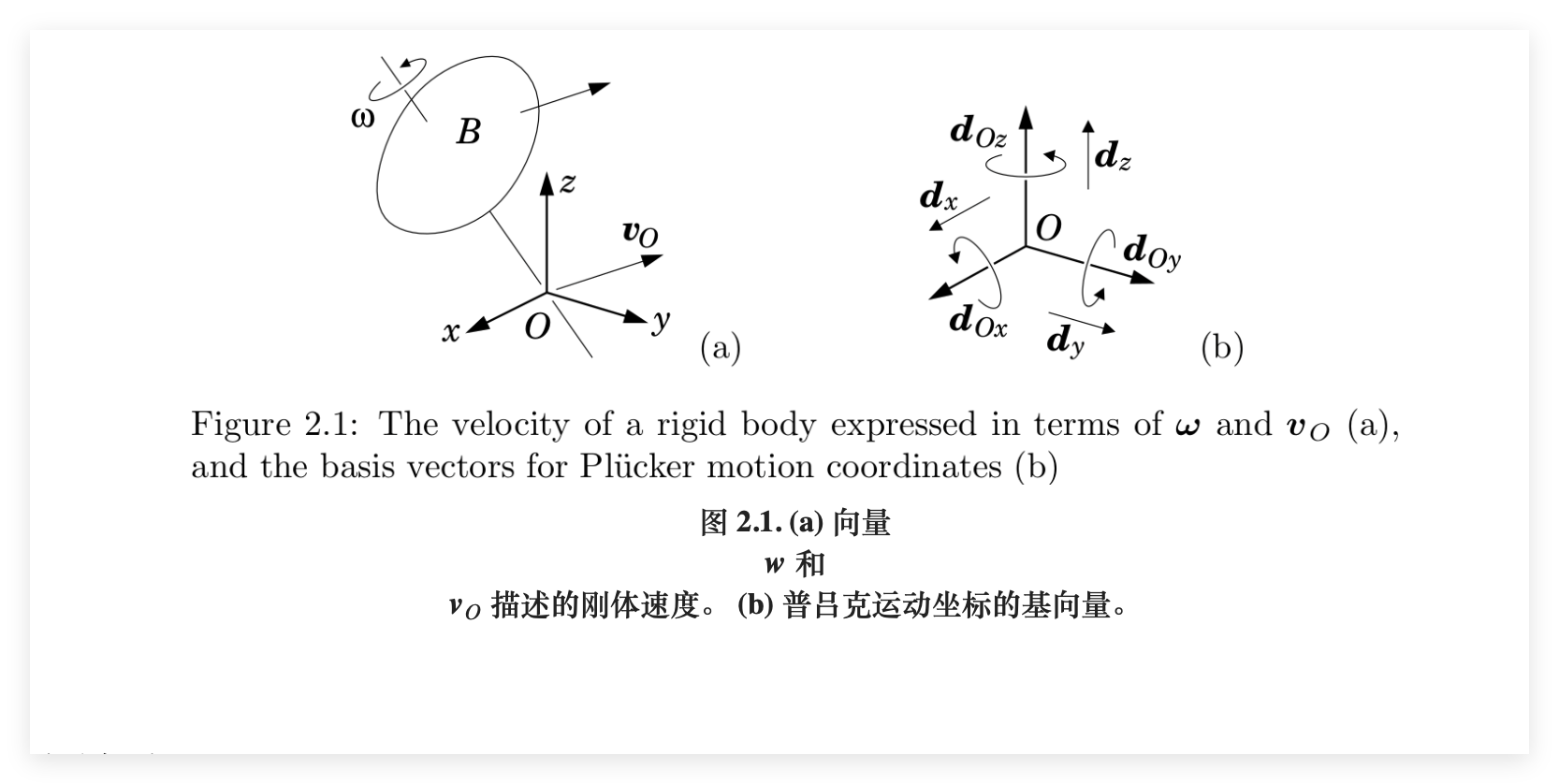
为了让抽象的子空间进入神经网络进行运算,普吕克坐标就是这里的选择。
通过一种被称为外积的操作,我们可以将两个向量所张成的平面编码为一个高维向量,就像是为每一个几何平面生成了一张唯一的uid,让神经网络能够像处理普通数据一样处理复杂的几何形态。
普吕克坐标必须遵循一组普吕克关系的代数方程,在模型训练中引入了一种强大的几何归纳偏置,通过强制中间表示满足这些几何定律,模型被约束在流形这一特定轨迹上进行学习。这种约束缩小了模型的搜索空间,以及避免了无效的参数更新,还能确保了模型生成的每一项表达在数学逻辑上都是严谨且具备几何意义的。
架构

第一步是线性降维,Transformer的原始数据维度很高,直接拿来做复杂的几何运算太慢了,这一步就是只保留最核心的特征,为了省计算量也是为了提取出适合在几何流形上操作的本质坐标。

第二步是多尺度局部匹配,像Attention那样我们要全局关注,这里我们只和特定距离的组队。比如“我”只和“我前这一个词”、“我前第四个词”组队,相当于在时间轴上开了几个特定大小的窗口,只看这些窗口里的局部关系。

第三步是格拉斯曼,把关系变成几何形状。在Attention里两个词的关系只是一个数字,但在 论文的模型里,两个词连成了一条线,模型计算这个平面的普吕克坐标。


第四步是Gated Fusion,模型有一个Gate类似水龙头,它决定是该多保留一点原来的记忆还是多采纳一点刚才算出来的几何推理结果?
对比
虽然格拉斯曼模型在理论上胜出了,但是目前硬件生态中还是面临硬件的劣势,毕竟英伟达的GPU是为密集矩阵乘法设计的,尽管是线性复杂度,当前的实现在中等长度序列上反而比优化的Transformer更慢。
从数学可解释性来讲两个就是不透明张量和几何不变量,Transformer解释性通常依赖于可视化Attention Map,但是Attention权重并不总是对应于人类理解的重要性,它是一个黑盒。
Grassmann解释性建立在几何之上,我们可以检查学习到的子空间的性质,普吕克关系提供了一种数学上的Sanity Check,模型被迫在流形上思考,内部状态更有结构性。
什么是推理?
Transformer将推理视为检索,问模型一个问题,模型在历史上下文中搜索相关信息,然后加权组合。
格拉斯曼架构将推理视为Flow或Deformation,信息被编码为几何对象,随着网络深度的增加,这些子空间在格拉斯曼流形上发生连续的变换。
深度学习的通用方法往往胜过特定结构,然而Attention Is Not What You Need认为在特定的任务中,强加正确的几何约束比单纯增加数据和算力更有效。Transformer是白板,它什么都不假设完全依赖数据来学习关系,Grassmann接近结构化先验,它假设关系具有几何结构。
硬件彩票
Hooker提出的硬件彩票理论是成功的算法往往是那些最适合当前硬件的算法,Transformer的胜利很大程度上是因为它契合了GPU的矩阵吞吐能力,格拉斯曼模型要想成功,需要数学上的证明,也需要编写高效的CUDA内核来并行化普吕克坐标的计算。
Attention Is All You Need的论文肯定是划时代的,但是也可能将领域锁定在了一个局部最优解上,现在花费了大量资金来建设基础设施来支持计算,这本身就构成了一种路径依赖,新的论文让我们明白目前的Transformer可能只是通过暴力计算掩盖了模型设计的低效。
风险
潜力很直观,对于整书分析 基因组测序 长期记忆Agent来说,线性复杂度是刚需。格拉斯曼方法提供了一种比单纯线性化Attention理论更好的路径,它在科学计算中找到杀手级应用,因为这些领域的底层规律本质上就是几何的。
风险在于局部窗口的限制,虽然论文声称多尺度可以缓解,但在数千个Token的距离上进行多跳推理,效率和精度是否能匹敌Transformer的一步到位还是没有定论。