姑且可以当作是一个最不喜欢的古法看论文环节,现在已经绕不开DeepSeek那篇MLA和低秩压缩了,虽然DeepSeek通过MLA在工程上有大的进步,但是这种进步还是需要像mHC这样的理论来提供数学解释。
读完mHC相关的论文&社区讨论之后,看到的是传统的残差连接会导致高维表征在深层网络中发生坍缩和畸变,未来的架构演进将不再是只增加参数,转而向如何通过流形约束来确保信息在传递过程中不背离数据本身的拓扑结构。
目前像长文本失效和偏见数据的瓶颈是因为我们一直试图用平坦的视角去强行处理弯曲的数据,我认为如果连接本身不再是线性的,AI可能会具备更强的逻辑外推能力。
在过去很长一段时间里的深度学习都是Transformer架构和以欧几里得向量空间为基础的数据表示,GPT-4和BERT这类自己常用模型都是建立在稠密张量计算和点积注意力机制上面。
现在模型规模增长太快了,大致找了三种技术搭配古法人工阅读法来作解析:BDH架构、格拉斯曼流形深度学习、基于黎曼几何的注意力机制公平性。
考虑到看这篇的几乎没有生物神经科学方向的朋友,所以BDH架构的我会直接跳过生物相关,只从算法效率和高维几何来解释。
在此之前回顾一下目前的局限性,Transformer的核心自注意力机制需要计算序列中所有Token两两之间的相互作用,时间复杂度和显存占用随序列长度N呈O(N^2)增长,所以限制模型处理超长上下文的能力。
主流算法是假设数据嵌入在平坦的欧几里得空间中,但是在实际操作的数据结构几乎都是非欧几里得特性,类似WordNet这样的层级关系可以自然嵌入双曲空间,像图片视频片段的变换不变性就构成了格拉斯曼流形上的子空间,如果强制将这些流形结构压扁到欧氏空间就会导致畸变。
还有一个是最近自己在做的时候发现的算法公平性,现在的线性投影去偏方法假设偏见是一个简单的线性向量,但是实际上偏见都是潜伏在非线性流形结构中,如果线性去除,既无法根除偏见还会破坏语义信息。
BDH - Bottleneck De-Hebbian
The Dragon Hatchling: The Missing Link between the Transformer and Models of the Brain
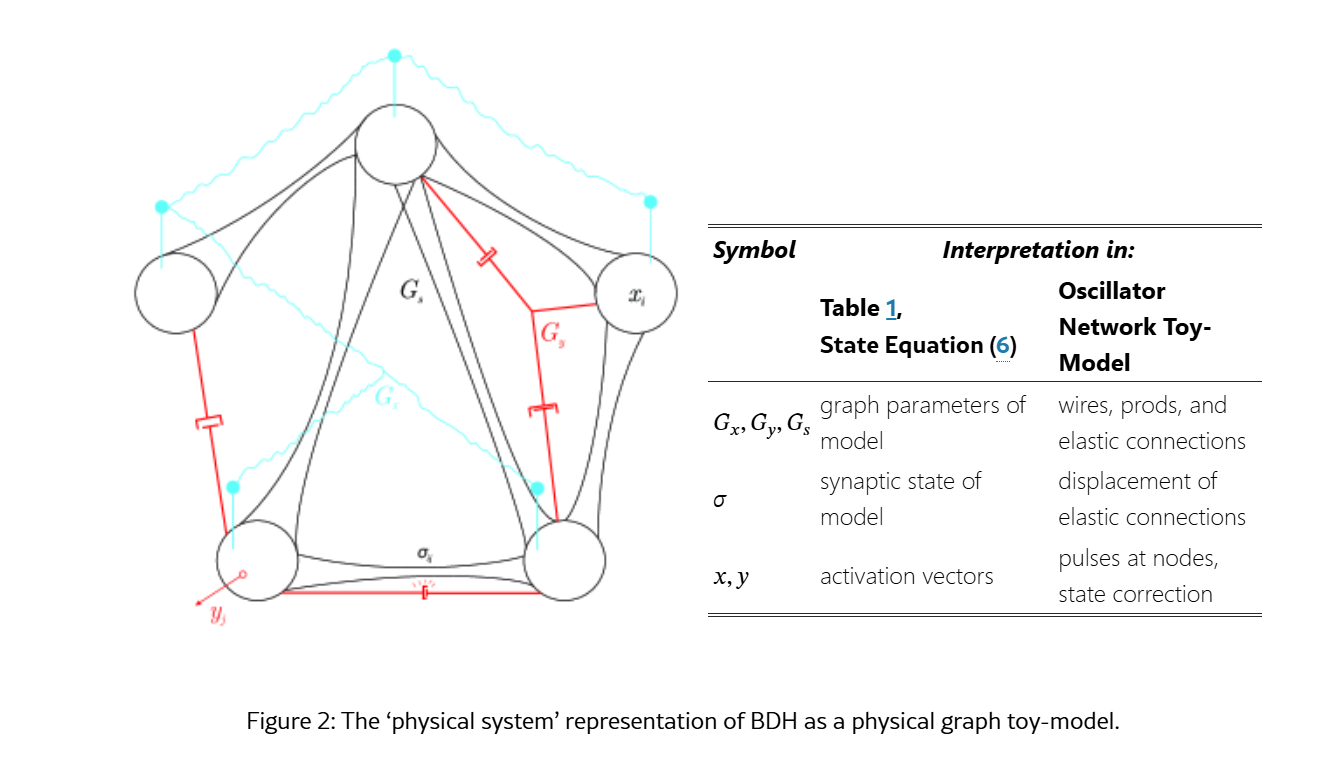
原文里面引用了好多生物大脑的名词,拿翻译器也看不懂所以忽略了,只从机器学习来看,BDH的BDH-GPU变体,是一种具有稀疏低秩约束的线性递归状态空间模型,它在数学上架起了GNN与稠密Transformer,提供了一种在保持高性能的同时将复杂度降低至O(N)的方案。
从稀疏图到低秩张量BDH的是否定Transformer中全连接的稠密矩阵乘法,它采用的是无标度网络启发的稀疏交互模式。在图论来看传统Transformer,它的注意力矩阵是一个完全图,BDH提出高效的信息处理应该基于稀疏图,其中少数Hub节点承担了大部分信息路由工作,在BDH-GPU实现中,这种稀疏图结构通过低秩矩阵分解来近似。
BDH架构
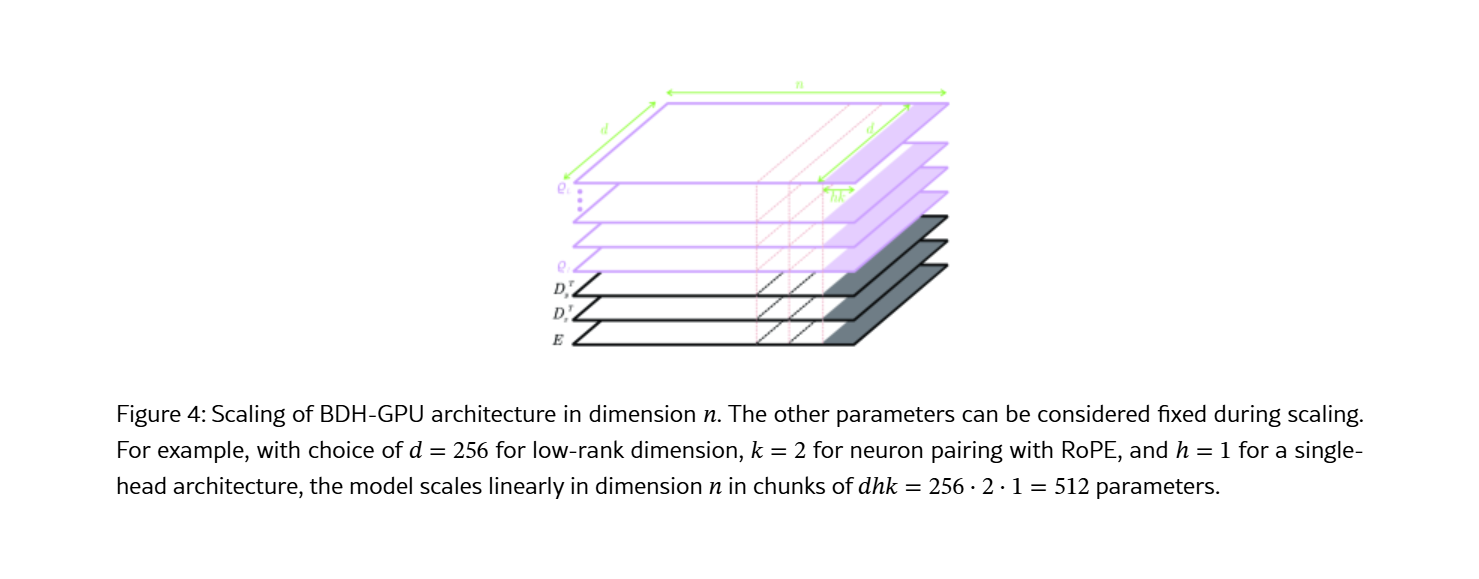
假设传统的网络层交互矩阵 W,维度为 [n x n],BDH不直接存储W,拆解为两个小矩阵相乘:
W ≈ D × E
- Encoder: 维度
[d x n],将高维特征压缩到低维瓶颈。 - D (Decoder): 维度
[n x d],从低维瓶颈重新广播回高维空间。 - d (Rank): 低维度的秩,满足 d 远小于 n。
这样参数量骤减,以及与LoRA微调的原理一样,但是BDH在预训练阶段就强制模型学习最浓缩的特征表示,产生稀疏且具备解释性的激活模式。
ReLU-Lowrank
BDH用ReLU-Lowrank Block来替代Transformer中的MLP。
#输入向量 x 维度 n
# E, D为低秩矩阵 b1, b2为偏置项
y = ReLU( D * ReLU( E * x + b1 ) + b2 )
这里的创新点在于通过双重ReLU,所有信号保持非负,就类似一种去噪机制,只要让强信号通过,诱导出类似L1正则化的特征稀疏性。
BDH还移除了传统的Softmax注意力,用线性递归更新。BDH维护一个固定大小的状态矩阵 S(就是Synapse
更新逻辑
写入状态:S(t) = λ * S(t-1) + (V_t ⊗ K_t)
⊗ 代表外积(Outer Product):将当前的键值对直接“印”在突触矩阵上。
λ 代表衰减因子:让模型更关注近期信息,起到隐式位置编码的作用。
读取输出:Output = S(t) * Q_t
Currency Synapse - 货币突触
货币突触是一种基于误差驱动的局部更新规则。在时间步 t,模型会:
- 根据当前状态 对下一个信号进行预测
- 计算预测值与实际输入信号之间的偏差
-
突触修正
Error = Input_Signal - Predicted_Signal S_new = S_old + Learning_Rate * (Error ⊗ Input_Signal)
叫货币的原因是强调流通性和即时价值,信息在状态矩阵中不断被熔了又重塑,以及模型在处理当前句子时会根据前文的语义偏差实时调整自己的注意偏好。
与Transformer对比
| 维度 | 传统Transforme | BCH Linear Recurrence |
|---|---|---|
| 权重状态 | 推理阶段模型参数完全冻结。 | 推理时状态矩阵 随输入实时演化 |
| 学习时机 | 学习仅发生在预训练阶段 | 推理过程本质上包含微型训练 |
| 上下文利用 | 从历史记录中查找相关片段 | 将新知识吸收进当前的突触中。 |
这种机制在数学上等于二阶优化,传统的注意力机制是线性读取,这里的货币突触是通过不断的误差修正使模型能够对上下文中的新模式产生极强的自适应能力,所以就是为什么BDH即使参数量小,也能在长文本对话中表现出高逻辑连贯性。
格拉斯曼流形
Deep Grassmannian multiview subspace clustering with contrastive learning
Research Collection School Of Computing and Information Systems
上面的BDH架构是在优化向量处理的效率,这里的格拉斯曼流形深度学习是在挑战一切皆向量这个基本假设。
在CV图像集分类里面的单一数据点是充满噪声的,而一组数据点张成的子空间才是包含了本质特征的稳健表示。
格拉斯曼流形 Gr(k, n) 定义为 R^n 空间中所有k维线性子空间的集合。
核心优势在于旋转不变性,在现在深度学习中处理视频片段我一般是拿RNN处理,不会注意到视频对象只是发生了旋转变换,这些点在欧氏空间坐标不同,但是张成的子空间是一样的。
商空间 Quotient Space
Gr(k, n) = St(k, n) / O(k)
格拉斯曼流形将所有仅相差一个正交旋转变换(O(k))的表示视为流形上的同一个点。算法意义是基于此流形的网络有内在旋转不变性,不需要依赖大量数据增强。
格拉斯曼网络的层级架构
- 投影映射层
这是输入层,负责将原始数据矩阵X映射到流形上,常用的数学表示是投影矩阵:
P = X * (X’ * X)^(-1) * X’
或者通过SVD分解后取左奇异向量,此时P是一个幂等对称矩阵,它唯一确定了一个子空间且对子空间内的基变换具有不变性。
- 全秩映射层
相当于欧氏网络中的全连接层,为了不让结果偏离流形,格拉斯曼网络采用带回缩的线性变换:
Y_out = Q_component( W * Y_in )
W是学习对子空间基向量的线性变换,Q_component是通过QR分解强制结果重新正交化,确保输出仍然位于流形上,可以说是像几何激活函数那样的作用。
- 投影池化层
在弯曲空间里的算术平均是无效的,格拉斯曼网络采用Karcher Mean:
- 均值 μ = 使所有样本点到 μ 的测地线距离平方和最小的点
虽然计算比欧氏均值贵,但是它可以生成在几何上中心子空间来聚合多帧信息。
2024-2025年的格拉斯曼对比学习
https://www.researchgate.net/publication/398891082_Deep_Grassmannian_multiview_subspace_clustering_with_contrastive_learning
顺带看了下最近两年的新研究,他们是将格拉斯曼几何与对比学习结合来用于多视图子空间聚类,创新点是投影度量损失。
传统的对比学习使用余弦相似度,格拉斯曼对比学习使用投影度量作为核心:
| **距离 d = (1 / √2) * | Y1Y1’ - Y2Y2’ | _F ** |
先流形嵌入,将不同视角的数据映射到格拉斯曼流形,然后最小化同一样本不同视角间的测地线距离,最大化不同样本间的距离,结果是网络学习到一个共识子空间自动剔除视角特定的噪声。
黎曼几何与注意力机制公平性
Riemannian Geometry for Fairness in Attention Mechanisms of Language Models
现在在用的方法是假设词向量空间中存在一个恒定的向量 v_bias,例如man和woman,只要将所有词向量投影到与向量正交的超平面上就可以消除偏见。
论文里面提到了偏见子流形Bias Submanifold
- 某些偏见是嵌入在层级结构中的,双曲空间比欧氏空间更能准确捕捉这种层级性。
- 词与词之间的共现统计量形成了对称正定矩阵流形,偏见表现为特定几何方向上的强相关性。
黎曼注意力机制
GyroAtt: A Gyro Attention Framework for Matrix Manifolds
传统的缩放点积注意力计算 Score = Q * K^T,黎曼注意力机制把这个替换成了流形上的测地线距离:
Attention(i, j) ∝ exp( - d^2(q_i, k_j) / τ )
其中d是黎曼流形上的测地线距离。
曲率的公平性正则化
这里引入了一个公平性正则化度量张量G(x):
G_fair(x) = G_base(x) + α * Σ [ 偏见损失的梯度 ]
先识别出流形上的像有种族歧视词汇的敏感区域,然后局部地拉伸黎曼度量,在敏感区域人为增加点之间的距离,由于距离变大,注意力机制分配给这种刻板关联的权重会自然地衰减。
之前传统的线性去偏方法,都是把偏见看作词向量空间中一个恒定的方向向量,通过硬性的正交投影从原始空间中抹除,这种强制抹除只能说在处理显性偏见时直接,但是在我之前做的东西上都或多或少会损伤正常的语义特征,而且由于假设偏见在空间中是线性分布的,我们难以修复嵌入在复杂层级结构隐性偏见。